算法复杂度基本概念

内容主要参考《算法导论》(原书第3版) 中第3章:函数的增长.
其在第17章中介绍了一些高级的分析方法,用来分析一些复杂问题的复杂度,这里暂时不做介绍,以后有机会另讲.

---

复杂度简介

所谓算法的复杂度,指的是一个算法所需要消耗的资源,通常包含时间资源(时间复杂度)和内存资源(空间复杂度).复杂度是评价算法的重要指标,它直接决定了算法的执行效率.
这里以时间复杂度为例.当一个问题的输入规模为$n$时(例如对一个含有$n$个数的数组排序),通常可以用一个函数$f(n)$表示算法在解决该问题的时候需要的基本操作次数,函数$f(n)$便可以代表一个算法的时间效率(通常我们认为一次基本操作所需的时间是一个常数).
比如对插入排序最坏情况的运行效率我们可以用一个多项式刻画:
$$f(n) = an^2 + bn + c$$
其中$a,b,c$是常量.
绝大多数情况下,我们并不需要知道精确的算法效率,而更加关心的是在大输入规模下算法运行时间的增长量级,也就是渐进效率.
例如上面的$f(n)$,可以看出当输入规模$n$足够大时,运行时间的增长主要受到$an^2$项的影响,甚至常数$a$本身的影响都可以忽略,因此我们可以用$n^2$来表示这个算法的渐进效率.

---

渐进记号

当然,我们还需要一些记号来表示渐进效率,我们常听说的$O(n)$等等就是用了其中一个记号.此外还有$\Theta,o,\Omega,\omega$,下面就给出一个形式化的定义:
$$\Theta(g(n)) = \{f(n):存在正常量c_1,c_2和n_0,使得对所有n \ge n_0,有0 \le c_1g(n) \le f(n) \le c_2g(n)\}$$
$$O(g(n)) = \{f(n):存在正常量c和n_0,使得对所有n \ge n_0,有0 \le f(n) \le cg(n)\}$$
$$\Omega(g(n)) = \{f(n):存在正常量c和n_0,使得对所有n \ge n_0,有0 \le cg(n) \le f(n)\}$$
$$o(g(n)) = \{f(n):存在任意正常量c和正常量n_0,使得对所有n \ge n_0,有0 \le f(n) \lt cg(n)\}$$
$$\omega(g(n)) = \{f(n):存在任意正常量c和正常量n_0,使得对所有n \ge n_0,有0 \le cg(n) \lt f(n)\}$$
公式比较抽象,看图来得直观一些(图片来自这里,和算法导论上的图一样):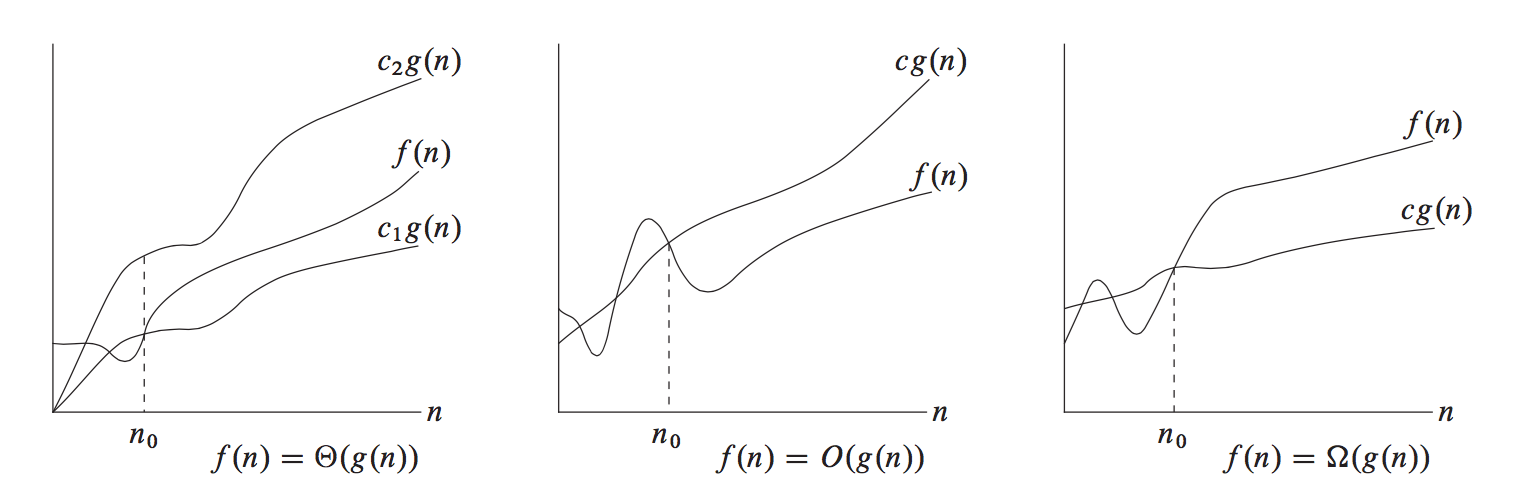

简单的说,$\Theta(g(n))$就是有$cg(n)$随着$c$不同的取值,既可以表示$f(n)$的上界,也可以表示$f(n)$的下界.$O(g(n))$意味着只表示上界,$\Omega(g(n))$意味着只表示下界.
例如以下式子都是成立的:
$$\Theta(n^2) = 2n^2 + 3n + 1$$
$$O(n^2) = 2n^2 + 3n + 1$$
$$O(n^3) = 2n^2 + 3n + 1$$
$$\Omega(n^2) = 2n^2 + 3n + 1$$
$$\Omega(n) = 2n^2 + 3n + 1$$
$$\Theta(g(n)) = f(n) \Leftrightarrow O(g(n)) = f(n) 且 \Omega(g(n)) = f(n)$$
而$o(g(n))$和$\omega(g(n))$意味着不是紧确界,例如有以下式子:
$$o(n^2) \neq 2n^2 + 3n + 1$$
$$o(n^3) = 2n^2 + 3n + 1$$
$$\omega(n^2) \neq 2n^2 + 3n + 1$$
$$\omega(n) = 2n^2 + 3n + 1$$
关于渐进函数,其有以下性质:
1.传递性
$$f(n) = \Theta(g(n)) 且 g(n) = \Theta(h(n)) \Rightarrow f(n) = \Theta(h(n))$$
$$f(n) = O(g(n)) 且 g(n) = O(h(n)) \Rightarrow f(n) = O(h(n))$$
$$f(n) = \Omega(g(n)) 且 g(n) = \Omega(h(n)) \Rightarrow f(n) = \Omega(h(n))$$
$$f(n) = o(g(n)) 且 g(n) = o(h(n)) \Rightarrow f(n) = o(h(n))$$
$$f(n) = \omega(g(n)) 且 g(n) = \omega(h(n)) \Rightarrow f(n) = \omega(h(n))$$
2.自反性
$$f(n) = \Theta(f(n))$$
$$f(n) = O(f(n))$$
$$f(n) = \Omega(f(n))$$
3.对称性
$$f(n) = \Theta(g(n)) \Leftrightarrow g(n) = \Theta(f(n))$$
4.转置对称性
$$f(n) = O(g(n)) \Leftrightarrow g(n) = \Omega(f(n))$$
$$f(n) = o(g(n)) \Leftrightarrow g(n) = \omega(f(n))$$

然而,这么多性质对于大多数人来说,除了用来找工作应试之外并·没有·什么·卵·用.

---

简单的估算复杂度

这里以简单的冒泡排序为例.

function bubbleSort (arr) {
	var n = arr.length, i, j, tmp;
	for(i=n-1;i>0;--i) {
		for(j=0;j<i;++j) {
			if(arr[j]>arr[j+1]) {
				tmp = arr[j+1];
				arr[j+1] = arr[j];
				arr[j] = tmp;
			}
		}
	}
	return arr;
}

print(bubbleSort([4,43,87,23,56,24,12,1]));

虽然是JavaScript代码,其实和其他语言也差不多.基本思路就是从后往前枚举数组中每个位置,让这个位置及其之前的数中最大的数”冒”上来.也就是从前往后枚举相邻的数,通过交换让较大的数排在后面.当处理完每个位置,整个数组就是有序的了.
第一次冒泡的效果如图所示:

简单分析一下这个输入规模是$n$(数组大小)算法.我们先看循环内的操作,有$1$次比较和$3$次赋值,而且赋值是否执行是由判断的结果决定的.但不管如何,操作次数是不大于$4$的.
然后我们来看循环.当外层循环$i=n-1$的时候$j$可以取$0$到$n-2$($n-1$次),当外层循环$i=n-2$的时候$j$可以取$0$到$n-3$($n-2$此),以此类推.所以循环次数的和可以看成是$1$到$n-1$的等比数列求和,就是$\frac{n(n-1)}{2}$.
综合看来,算法的效率可以表示为:
$$f(n) = 4 × \frac{n(n-1)}{2} = 2n^2 - 2n$$
用渐进记号$O$表达就是(最直观的方法就是把多项式中增长最快的项拿出来,其他项和常数统统扔掉就可以):
$$f(n) = \Theta(n^2)$$
也就是说,冒泡排序的复杂度是$\Theta(n^2)$,当然满足$O(n^2)$
当然前面这些分析其实省略了一些操作,比如n,i,j的赋值,循环结束条件的比较等,但是反正要用渐进记号表示嘛,这些加进来也只是增加常数和低次项而已,最后都要扔掉,加上我又比较懒…
嘛,总之我们可以发现,其实影响最终渐进复杂度的只有枚举的次数而已,其他都是常数,通常分析复杂度只要分析枚举的次数就可以了.

我们再看一个改进版本的冒泡排序.

function bubbleSort2 (arr) {
	var n = arr.length,
		i,
		j,
		tmp,
		isSwap;
		for(i=n-1;i>0;--i) {
			isSwap = false;
			for(j=0;j<i;++j)
				if(arr[j]>arr[j+1]) {
					tmp = arr[j+1];
					arr[j+1] = arr[j];
					arr[j] = tmp;
					isSwap = true;
				}
			if(!isSwap)
				break;
		}
			
	return arr;
}

print(bubbleSort2([4,43,87,23,56,24,12,1]));

改动很简单,只是在外层循环加了一个跳出条件:当一轮冒泡时没有执行交换,说明前面所有的数字已经有序了,所以无需进行其他循环.
可以很容易发现,当原数组有序的时候,外层循环只需要执行一次就跳出了,因此最好情况下时间复杂度是$\Theta(n)$.同时,如果原数组逆序的话,则成为了最坏情况,复杂度是$\Theta(n^2)$.所以,对于任意规模为$n$的输入,我们都可以称这个算法的复杂度是$O(n^2)$,这意味着不管怎样的输入,算法运行时间的上界是$O(n^2)$.
往往我们在分析算法时更关心一个算法运行时间的上界,这也是为什么渐进符号$O$这么常见.

最后列举几种常见的复杂度:
$O(2^n)$ 常见于状态压缩,用二进制的$0$和$1$表示是否存在.
$O(n^x)$ 常见于循环,$x$代表有几层循环.
$O(log(n))$ 常见于树状结构的查询,某进制下的位枚举或者分段.
$O(1)$ 常见于简单公式计算或者简单的判断分支.