最长回文串是一个经典问题,要求对给定的字符串,找出其中的一个最长子串,满足其顺序和逆序相同.例如对于原字符串$aaaabaa$,其最长回文子串是$aabaa$.
对于这个问题(例题可以戳这里),一般有$O(n^2)$的暴力或DP解法,$O(n\log(n))$的后缀树解法,以及下面要讲的$O(n)$的manacher.
首先,回文串的奇偶问题对于编程来说一直是个麻烦事,因为一个回文串既可以以一个字符为中心(如$abcba$),也可以以两个字符中间为中心(如$abccba$).为了方便处理,manacher在原串的每个字符间中加入一个原串中没有的字符(包括开头和结尾).例如原串为$aaaabaa$,我们加入#,那么新串就是#$a$#$a$#$a$#$a$#$b$#$a$#$a$#.这样做的好处是,当我以#为中心查找最大回文的时候,对应就是原串中以字符间为中心查找;当以某字符查找的时候,对应在原串中以此字符为中心查找,只是最后找到的长度翻倍了而已.例如上面的新串可以找到最长回文串#$a$#$a$#$b$#$a$#$a$#,长度为$11$,而在原串中为$\lfloor\frac{11}2\rfloor=5$
接下来我们定义”回文半径”.所谓回文半径,指的是回文串从中心到其一个端点中含有的字符数量(包含端点),如#$a$#$a$#$b$#$a$#$a$#的回文半径是$6$.容易发现,一个点在新串的最长回文半径$r$比原串对应位置的最长回文子串长度$l$多$1$,即$l=r-1$.
我们用一个数组表示以每个位置为中心能得到的最长回文半径
如果能计算出这个数组,那么只要遍历一下找到最大值,便可以得到最长回文子串.
如果暴力的计算这个数组的话,复杂度就成$O(n^2)$了.而manacher从前往后计算这个数组,利用前面已经计算出的结果来减少后面的计算.
我们用$s[i]表示串中位置为$i$的字符,$r[i]$表示其回文半径.如果已知位置$r[id],则有$s[id+1]=s[id-1],s[id+2]=s[id-2],…,s[id+r[id]-1]=s[id-r[id]+1]$,即有对称性.这个性质也暗示着,对称位置的回文半径存在的某种联系.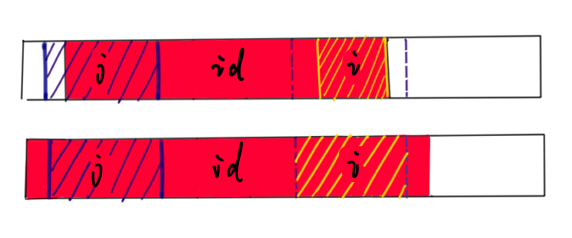
如图, 假设位置i和j相对于id是对称的, 红色部分为id的最大回文范围, 蓝色部分为j的最大回文范围, 蓝色的虚线表示j的最大回文范围相对id对称的位置. 当有了这些信息以后, 我们可以根据对称性得到黄色的部分, 其为i可能的最大回文范围.
之所以说是可能, 因为在图片中第一种情况下, i实际的最大回文范围可能比黄色部分还要大, 但是实际能继续扩大多大已经无法从已知的回文半径推断, 因此需要我们枚举去比较.
那么我们要找位置i的最大回文长度时我们应该用哪个位置作为id呢?
首先, 我们需要id的回文半径能够覆盖到i;
其次, 我们如果希望最后枚举比较的次数尽量的少, 应该使得id + r[id] - 1尽可能的大, 这样才能保证上图中第一种情况下我们算出的i可能的回文半径尽可能大.
综上, 我们其实只要使得id + r[id] - 1尽可能大就可以了.
这样manacher算法的流程就算是成型了, 下面是代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
using namespace std;
typedef long long ll;
int n;
string _s;
int gao(){
cin>>_s;
// 处理字符串奇偶问题, 前面和后面又多加了两个不会出现的字符, 用来避免越界, 减少后面循环里的判断
string s = "$#";
for(int i=0;i<_s.length();++i) {
s.push_back(_s[i]);
s.push_back('#');
}
s.push_back('&');
// mx表示max(id+r[id])
int mx = 0;
int id = 0;
vector<int> arr(s.length()-1,0);
for(int i=1;i<s.length()-1;++i) {
if(mx>i)
arr[i] = min(arr[2*id-i],mx-i); //位置i在id的回文范围内, 直接根据对称性得到一个可能的半径
else
arr[i] = 1; //回文半径至少为1, 将1作为可能的回文半径
// 从可能半径大小开始枚举比较, 得到真正最大回文半径
while(s[i+arr[i]]==s[i-arr[i]]) {
++arr[i];
}
// 更新mx和id
if(arr[i] + i > mx) {
mx = arr[i] + i;
id = i;
}
}
// 从求出的最大回文半径数组中得到最大值
int ret = 0;
for(int i=0;i<s.length()-1;++i) {
ret = max(ret,arr[i]-1);
}
printf("%d\n",ret);
}
int main()
{
scanf("%d",&n);
while(n--) {
gao();
}
}
最后再来说下复杂度.
从代码中可以看出, 外层for循环执行的次数肯定是O(n)的, 关键是内层的while循环.
只有两种情况可能多次执行while循环: mx <= i或者arr[i] == mx-i(图中第一种情况), 这就意味着mx会更新, 而且循环每执行成功一次, mx增大1.
而由于mx只会增加而且最大不会超过新串长度, 所以while总共的执行次数也是O(n), 所以整体复杂度是O(n).